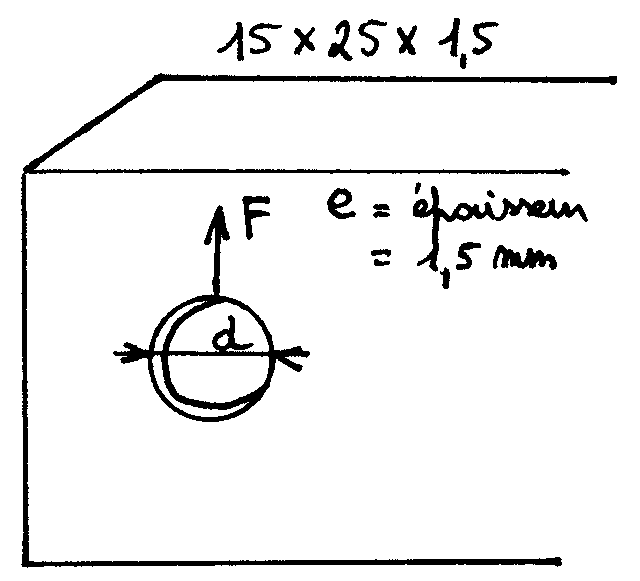Présentation Cager un parapente Evolution des modèles Détails techniques Calculs de résistance
12.1) Calculs ( cage Boréa 2004):
Donnée importante: Les parapentes sont prévus pour tenir à 8g (8x le poids du pilote) avant rupture.
A) Té à Titi:
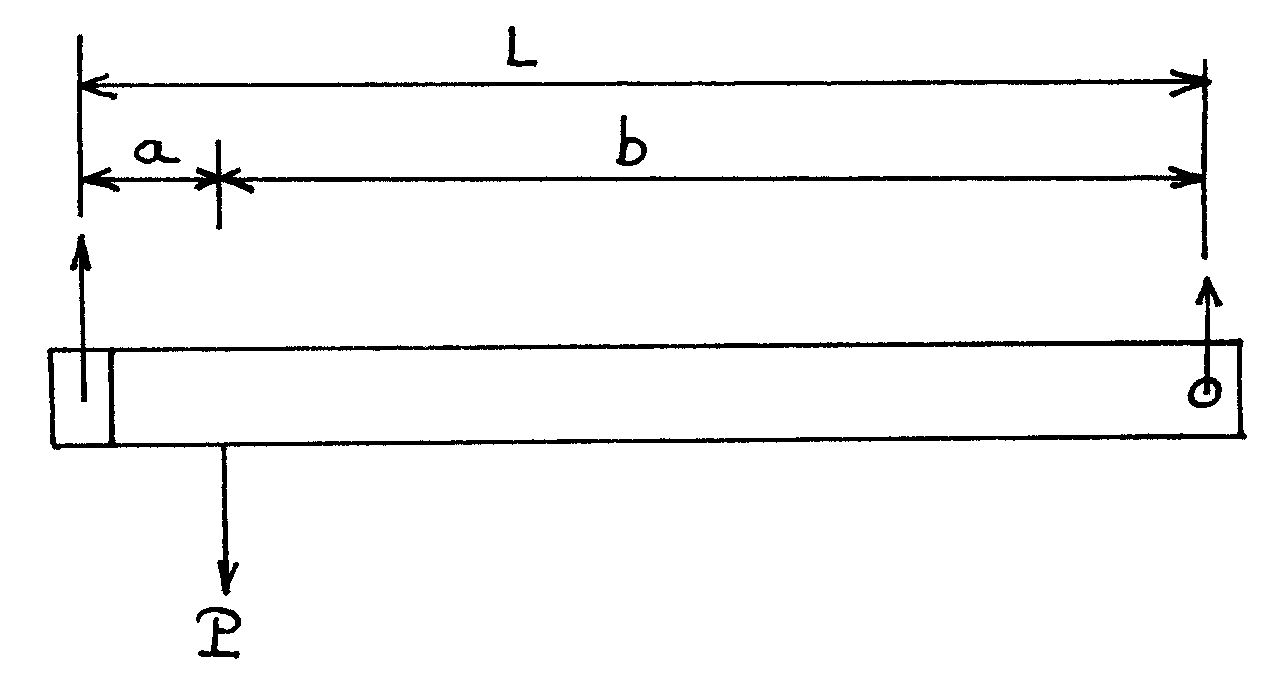
Le té à titi, est l'endroit où le pilote est accroché sous la cage en un point unique.
Ce sont les dimensions de celui ci qui rendent la cage plus ou moins facile à piquer, cabrer ou tourner.
A.1) Données: - Longueur(L): 31.75 cm / a = 2.75 cm / b = 29 cm
- Charge(P): 100Kg x 8g = 800 Kg x 10 = 8000 Newtons.
- Contrainte de traction et de flexion de rupture de l'acier inox utilisé: Sigma = 50 000 N / cm²
A.2) Calculs dans le sens de la longueur:
Charge localisée : P = Force pesanteur ( poids du pilote )
Moment fléchissant: Mf = (P x a x b) / L Mf = (8000 x 2.75 x 29) / 31.75 = 20 094.5 Ncm
I / V = Mf /sigma I / V = 20 094.5 / 50 000 = 0.4 cm³
Nous utiliserons du tube inox 15 x 25 x 1.5 mm dont le I / V = 0.72 cm³ car nous le déforcerons
légèrement avec les trous
de diamètre 6 mm pour le positionnement de la sangle du pilote. ( voir photo ci dessus )
A.3) Dans le sens de la largeur:
L'entraxe de la Boréa est de 17.5 cm, la Fiery 15 cm et la Seagull 12 cm.
Mf = ( 8000 x 8.75 x 8.75 ) / 17.5 = 35 000 Ncm
I / V = 35 000 / 50 000 = 0.7 x 83 % ( proportion du poids du pilote sur l'avant) = 0.58 cm³
Le tube utilisé à un I / V = 0.72 cm³ donc pas de problème.
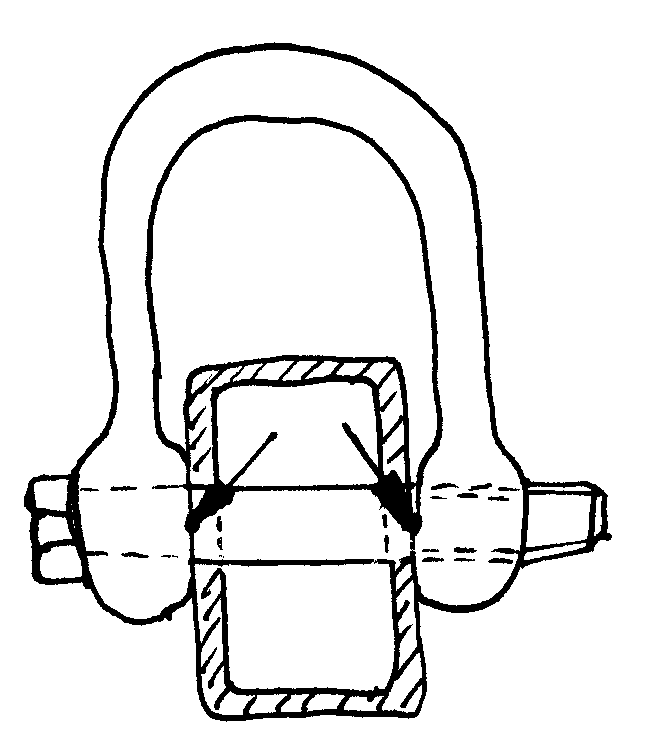
A.4) Pénétration de l'axe des manilles dans le tube inox: Contrainte de refoulement = F / ( d x e )
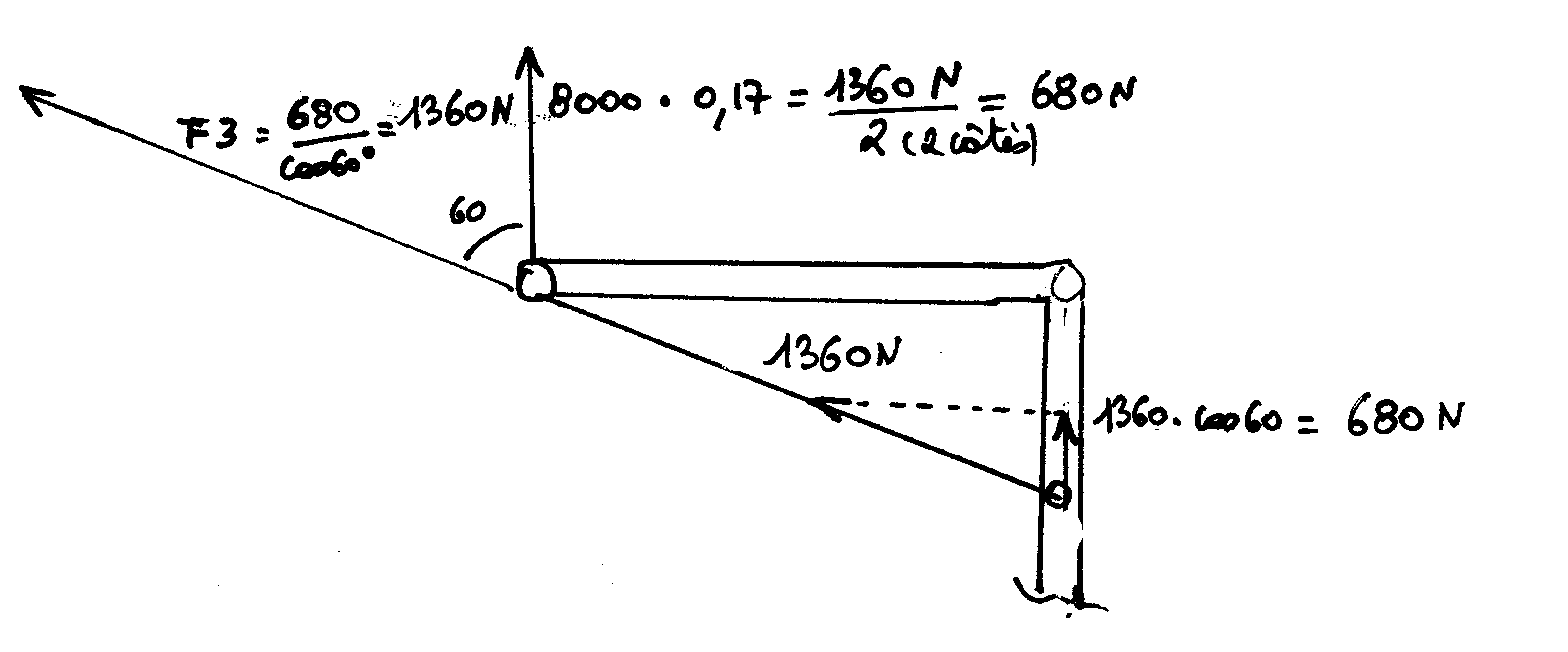
A.5) Charge sur une sangle avant: 83 % / 2 = 41.5 % du pilote ( 8000N x 41.5 % = 3320 N )
A.6) Charge sur la sangle arrière: 17 % du pilote ( 8000N x 17 % = 1360 N )
( Pourcentage calculé sur base du centrage: soit au neutre = vitesse bras haut du parapente)
Les sangles utilisées sont garanties par le fabriquant pour 1.5 tonnes minimum; soit 15000 N,
donc pas de problème.
A.7) Epaisseur du tube minimum acceptée:
e = F / ( d x contrainte de refoulement) or la contrainte de refoulement = 2 x la contrainte de
cisaillement. La contrainte de cisaillement = 4/5 de la contrainte de traction vue ci dessus.
Contrainte de refoulement = 2 x (4/5 x 50 000) = 80 000 N
Epaisseur = 3320 / ( 0.8 x 80 000 ) = 0.052 cm = 0.5 mm Or nous avons 1.5 mm x 2 côtés d'où pas
de problème.
Les manilles utilisées sont de diamètre 8 mm et de résistance à la rupture de 1600 Kg. L'écartement
intérieur est de 16 mm.
A.8) Cisaillement de l'axe de la manille:
Contrainte de cisaillement à la rupture: 4/5 x 50 000N = 40 000N
Charge = 3320 N pour 100 Kg à 8g ( voir ci dessus )
Section minimum de l'axe pour un cisaillement double = 3320 / 40 000 = 0.083 cm² ou 8.3 mm² / 2
or les axes ont une section de
( 3.14 x 8² ) / 4 = 50 mm² donc pas de problème.
A.9) En conclusion, le té de suspension à les caractéristiques suivantes:
- Matière: Inox de 50 000 N/cm² de résistance à la traction.
- Profilé 25 x 15 x 1.5 mm
- poids du tube seul: 480 grammes
- Longueur d'entraxe: 31.75 cm
- Largeur d'entraxe: 17.5 cm
- Manilles en acier inox de 8 mm
- Axes des manilles en acier inox calé avecde du loctite fort ( rouge )
- Sangles plates de 2.5 cm de large et 1.5 tonnes de résistance minimum.
- Mousqueton automatique 2.5 tonnes
B) La cage:
B.1) Calcul des tubes avants et arrières:
Comme nous l'avons vus plus haut, la charge est de 83 % sur l'avant ( 8000 N x 0.83 = 6640 N ) et de 17 %
sur l'arrière de la cage
( 8000 N x 0.17 = 1360 N ). Nous ne calculerons donc que le cas le plus défavorable, soit l'avant.
La contrainte de flexion de l'aluminium utilisé pour les tubes est de 11 000 N / cm²
Pour une charge répartie, P n'est plus égale au poids du pilote en Newtons mais à la charge par
cm de tube.
Les formules sont différentes.
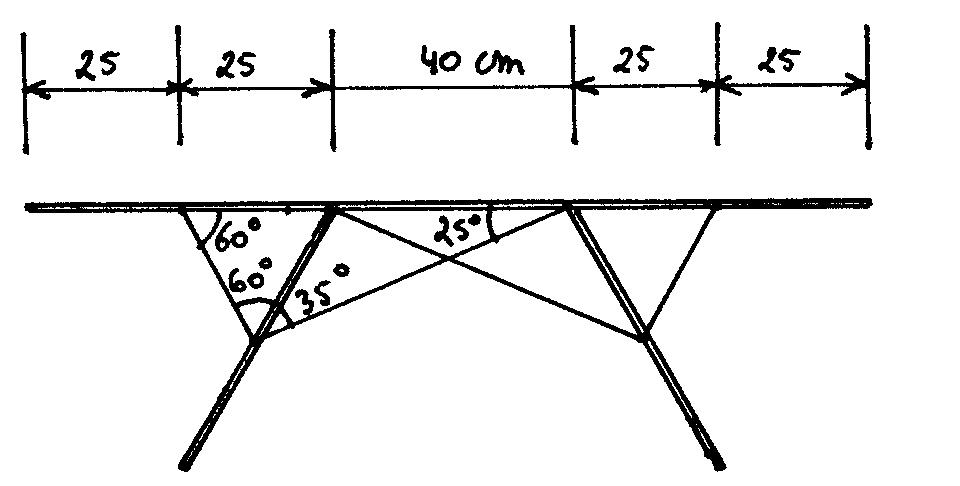
Charge répartie par cm : P = F / L totale P = 6640 N / 140 cm = 47.42 N/cm
La plus grande longueur sur deux appuis : 40 cm
Mf = ( P x L² ) / 8 Mf = ( 47.2 x 40² ) / 8 = 9484 N/cm
I / V = Mf / contrainte de flexion de l'alu. I / V = 9484 / 11 000 = 0.86 cm³
Rayon moyen du tube d'aluminium nécessaire: racine carré de ( ( I / V ) / ( 3.14 x e ) )
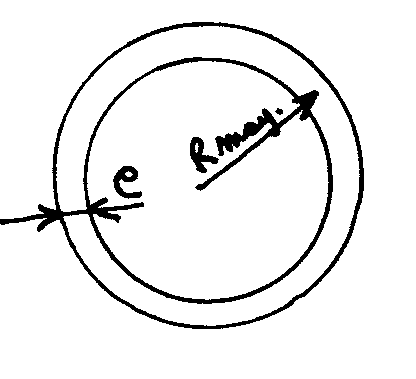
R moy. = racine carré de ( ( 0.86 ) / ( 3.14 x 0.2 ) ) = 1.17 cm
Diamètre = 2.34 cm
Nous utilisons dans cette partie de la cage du tube diamètre 2.5 cm doublé.
Le I / V de ce tube doublé est de ; 3.14 x e x r² = 3.14 x 0.4 x 1.05² = 1.4 cm³ pour 0.86 cm ³ calculé.
Les raisons sont : - Charge plus au centre que sur les bords.
- Tube déforcé par les attaches de suspentes de 5 mm de diamètre.
- Le poids du pilote se reporte sur moins de suspentes et plus au centre avec
les oreilles de la voile.
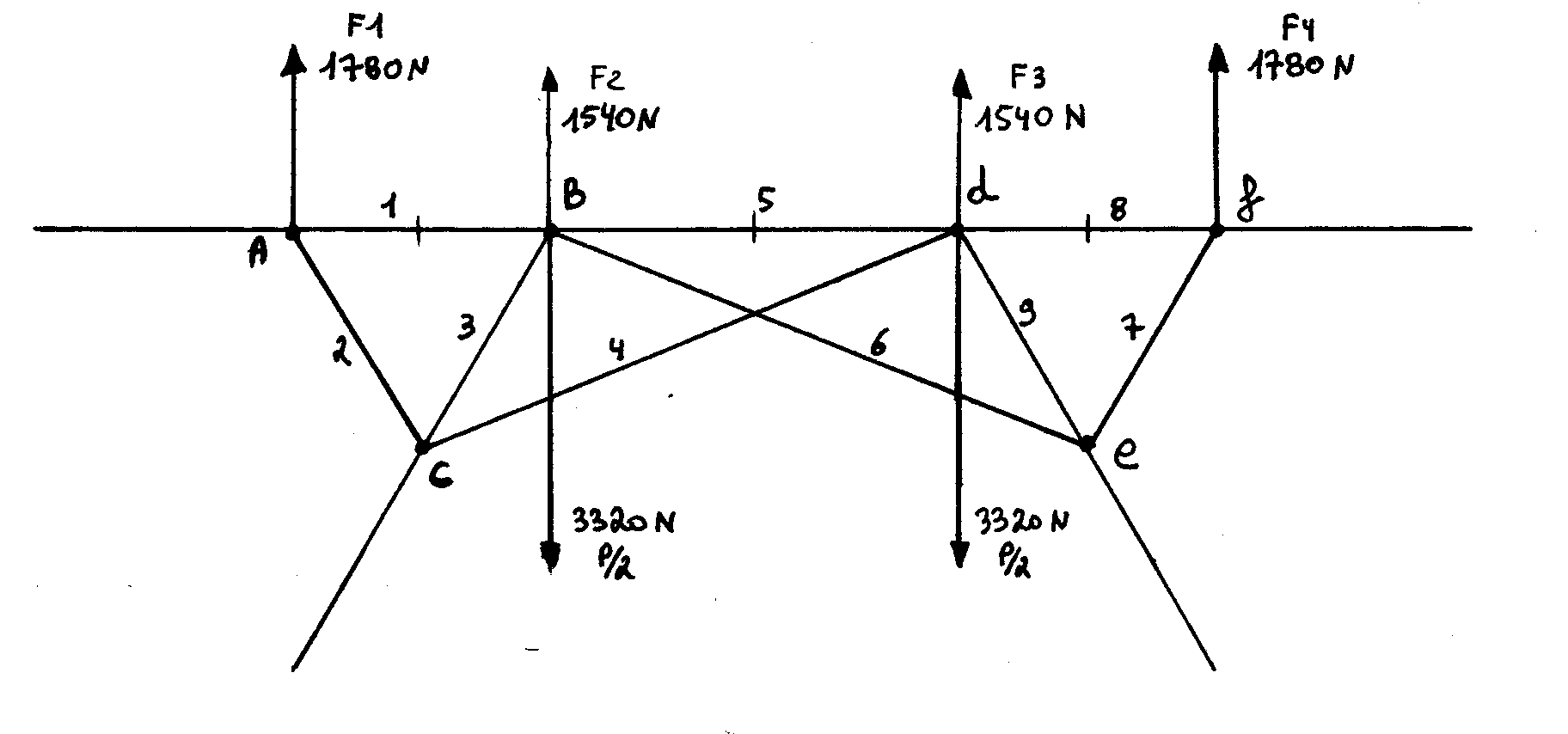
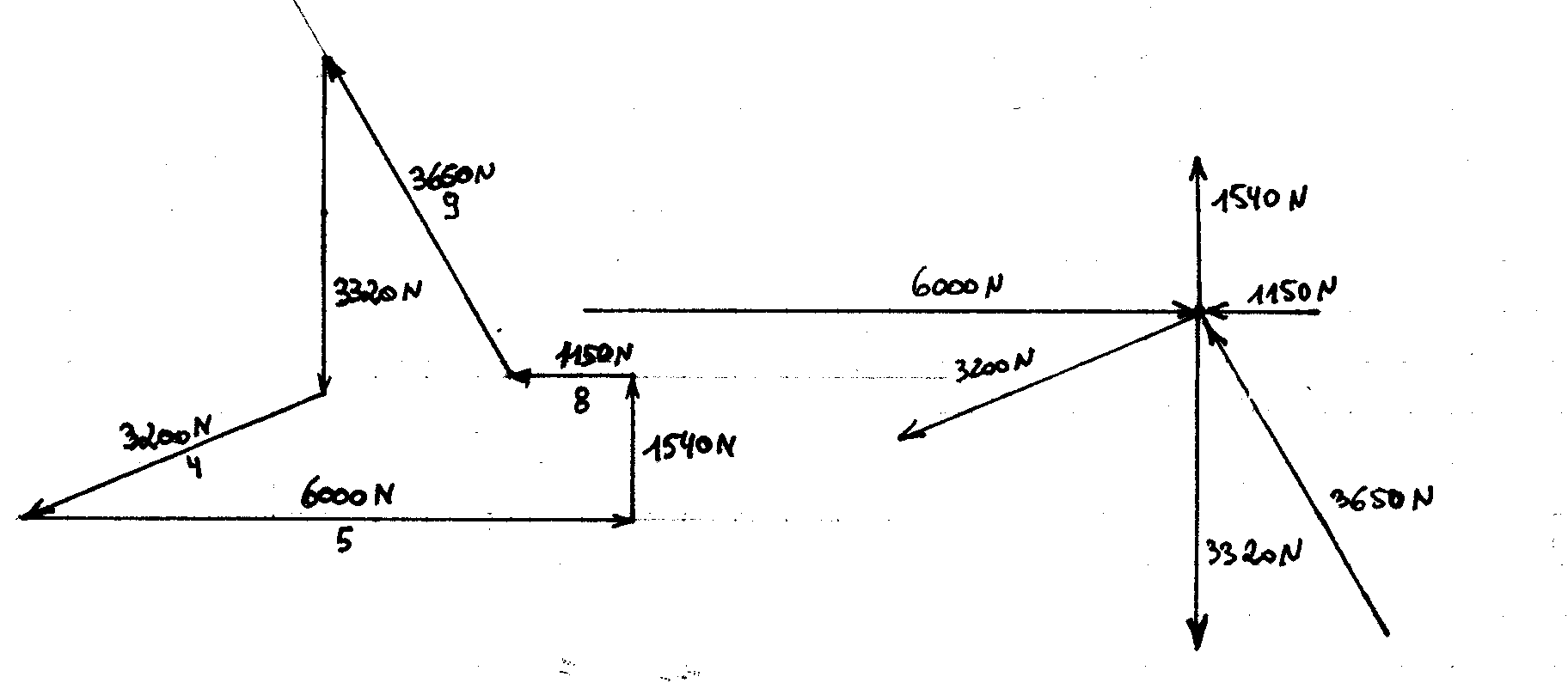
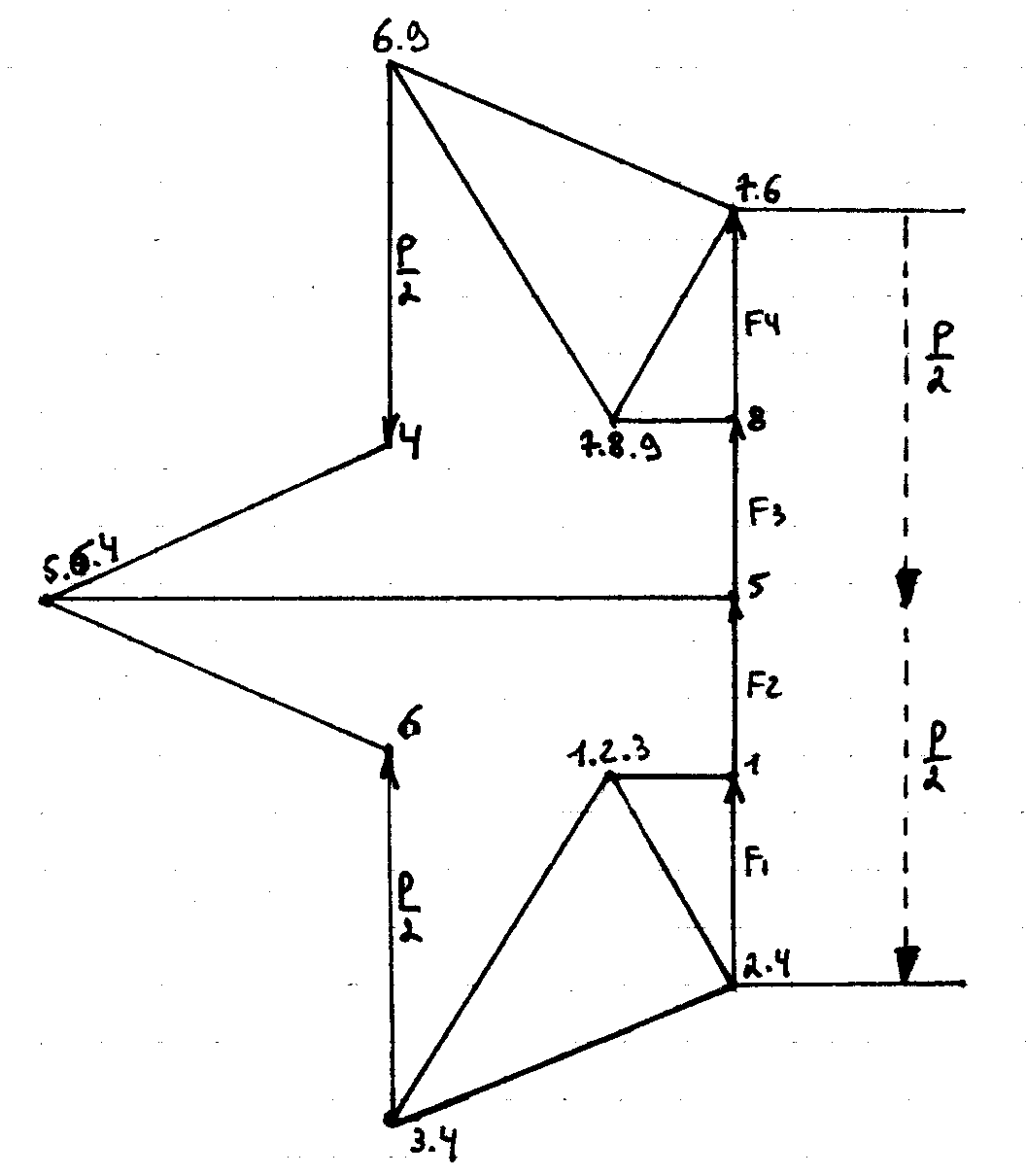
B.2) Calcul du système triangulé par la méthode Cremona:
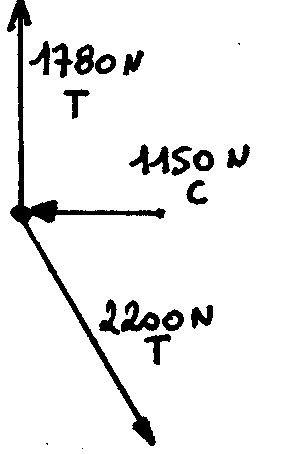
Noeud a: Polygone des forces: Inventaire des forces sur le noeud:
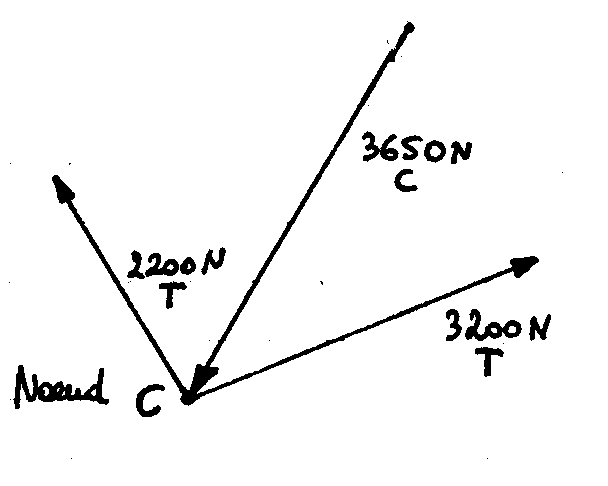
Noeud c: Polygone des forces: Inventaire des forces sur le noeud:
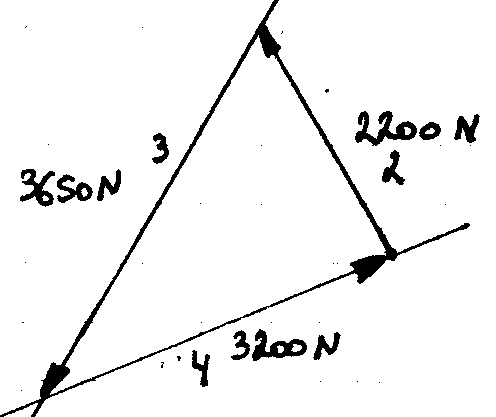
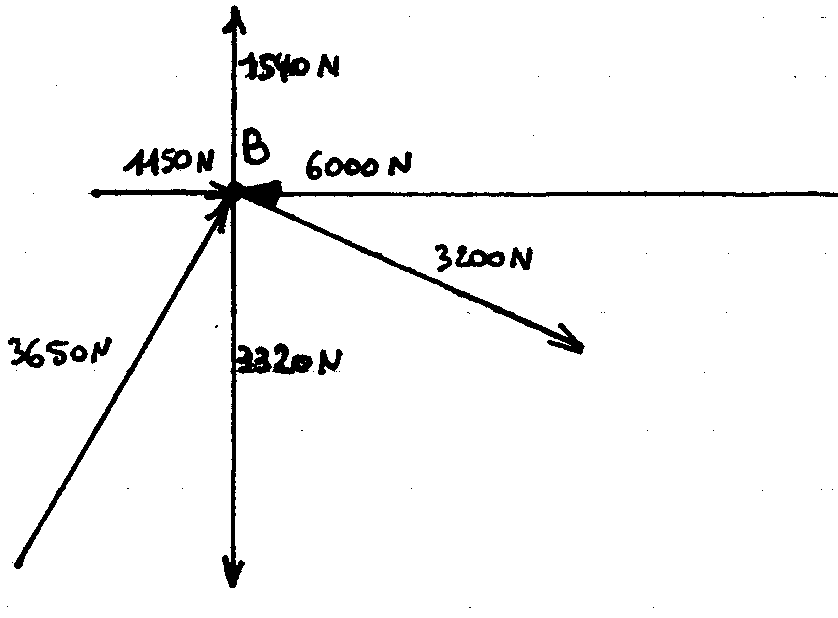
Noeud b: Polygone des forces: Inventaire des forces sur le nud:
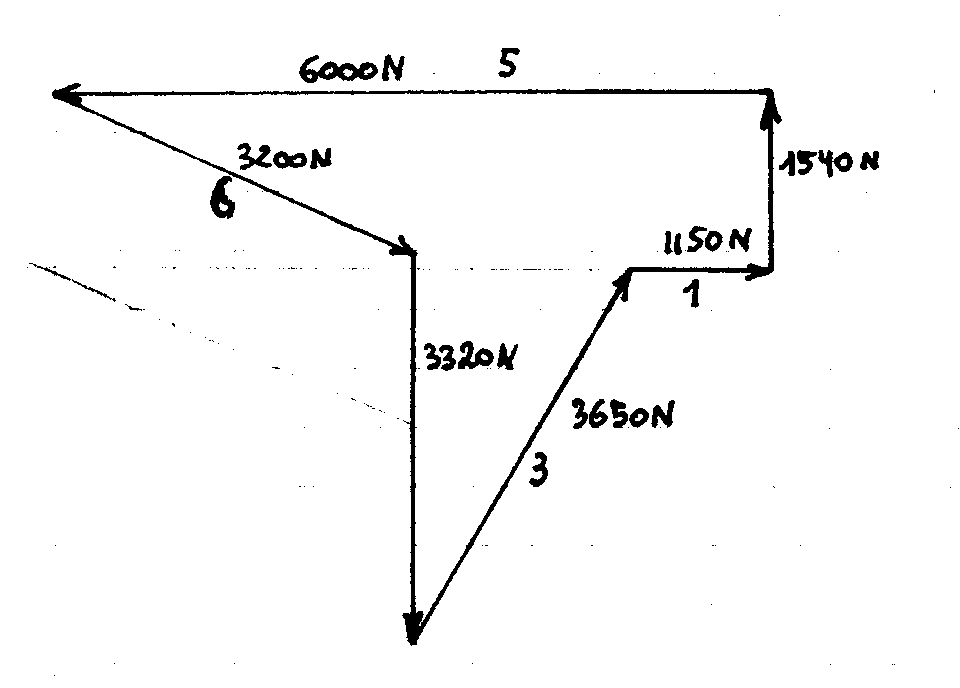
Noeud d: Polygone des forces: Inventaire des forces sur le noeud:
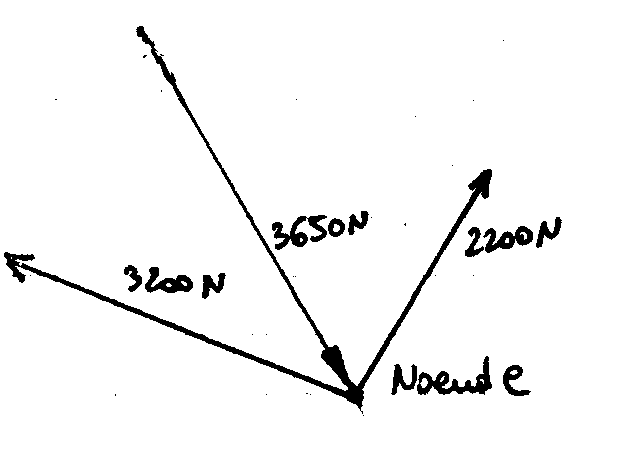
Noeud e: Polygone des forces: Inventaire des forces sur le noeud:
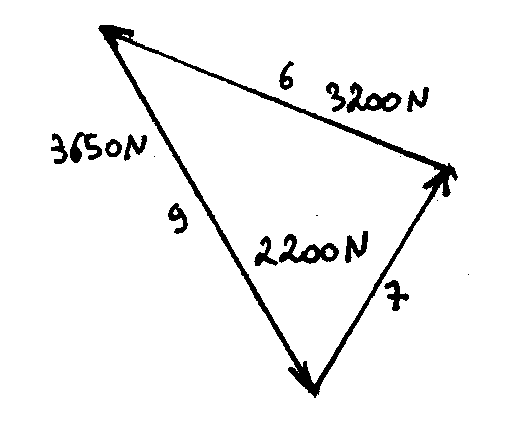
Noeud f: Polygone des forces: Inventaire des forces sur le noeud:
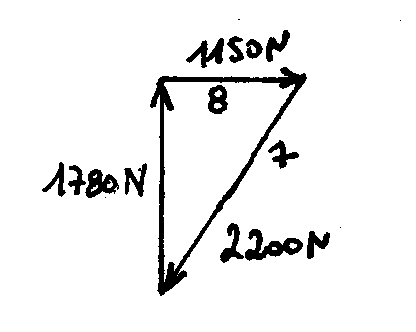
Epure de Cremona:
Conclusion:
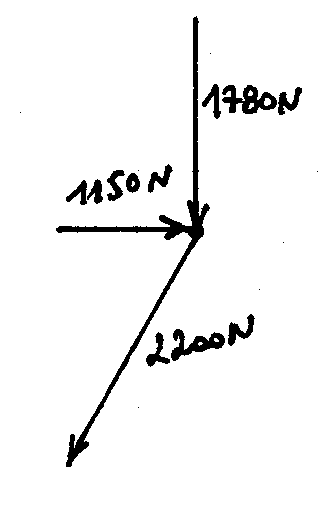
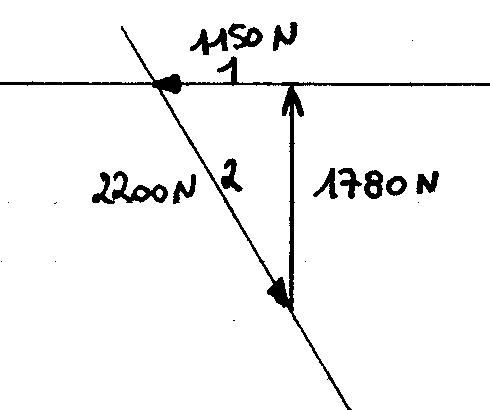
Effort de traction dans les câbles 2 et 7: 2200 N
Effort de traction dans les câbles 4 et 6: 3200 N
Effort de compression dans les lyres: 3650 N
Effort de compression dans les tubes 1 et 8 : 1150 N
Effort de compression dans le tube 5 : 6000 N
Les efforts de flexions sont étudiés dans les autres parties.
B.3) Vérification en compression du tube 5:
Effort total de compression = 6000 N
Contrainte de compression de l'aluminium utilisé: 11 000 N / cm²
Section minimum = F / contrainte = 6000 / 11 000 = 0.55 cm² = 55 mm²
Section du tube utilisé = ( 3.14 x ( 2.5² - 1.7² ) ) / 4 = 2.6 cm² = 260 mm² donc pas de problème
Contrôle au flambage:
Allongement = 40 / 2.5 = 16
Coefficient de fixation = 1
Correction au flambage : 0.97
Section corrigée : 55 / 0.97 = 57 mm²
Or nous avons 260 mm² ( voir ci-dessus) donc pas de problème.
Epaisseur du tube minimum acceptée:
Le vis de diamètre 0.8 cm pourrait rentrer dans l'aluminium et ovaliser le trou ou déchirer le tube.
e = F / ( d x contrainte de refoulement) or la contrainte de refoulement = 2 x la contrainte de
cisaillement. La contrainte de cisaillement = 4/5 de la contrainte de traction vue ci dessus.
Contrainte de refoulement = 2 x (4/5 x 11 000) = 17 600 N
Epaisseur = 6000 / ( 0.8 x 17 600 ) = 0.43 cm = 4.3 mm Or nous avons 4 mm x 2 côtés x deux vis
= 16 mm d'où pas de problème.
B.4) Calcul des câbles numéro 2 et 7:
Effort dans le câble: = 2200 N
Section du câble = F / contrainte de traction de l'acier inox
S = 2200 / 50 000 = 0.044 cm² = 4.4 mm²
Diamètre du câble: racine carrée de (( 4 x S ) / 3.14 ) =
racine carrée de (( 4 x 0.044 ) / 3.14) = 0.23 cm = 2.3 mm
Nous prendrons du câble inox de 3 mm de diamètre.
B.5) Calcul des câbles numéro 4 et 6:
Effort total dans le câble = 3200 N
Section du câble = 3200 / 50 000 = 0.064 cm² = 6.4 mm²
Diamètre du câble = racine carrée de (( 4 x 0.064) / 3.14 ) = 0.28 cm = 2.8 mm
Nous prendrons aussi du câble inox de 3 mm de diamètre.
B.6) Les attaches de suspentes:
Nous n'avons pas calculés les illets d'attaches de suspentes, nous les avons testés en
traction avec une charge de 80 Kg .
sans atteindre la limite élastique du matériau.
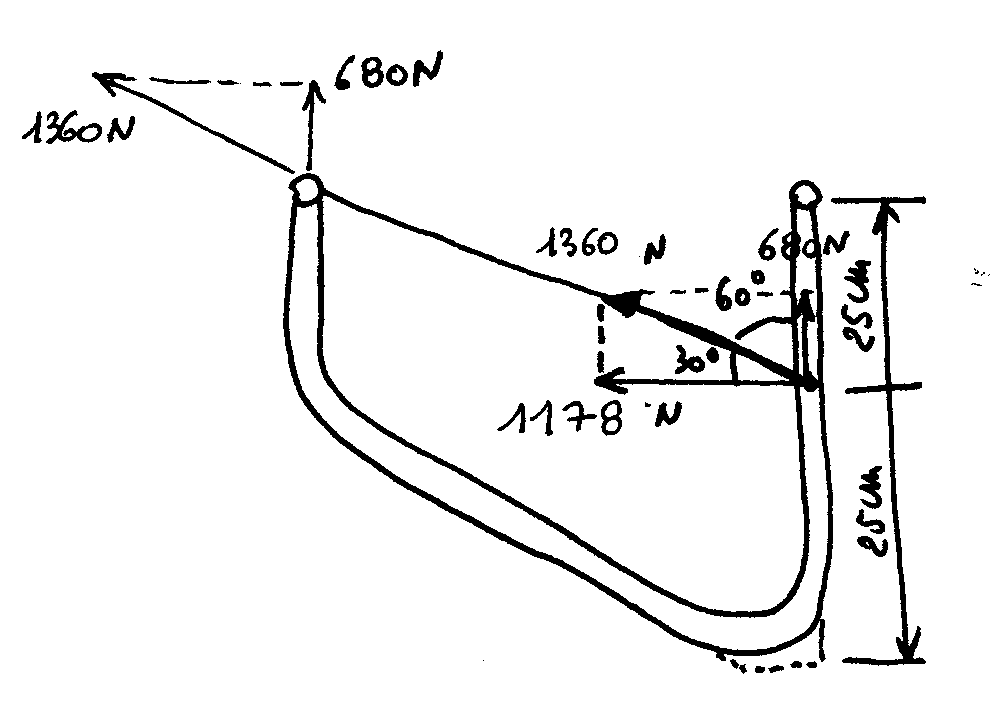
C) Les lyres:
C.1) Calcul de la lyre en compression:
Effort calculé par Cremona: 3650 N
Effort du au câble arrière:
Effort total de compression = 3650 N + 680 N = 4330 N
Contrainte de compression de l'aluminium utilisé: 11 000 N / cm²
Section minimum = F / contrainte = 4330 / 11 000 = 0.4 cm² = 40 mm²
Section du tube utilisé = ( 3.14 x ( 2.5² - 1.7² ) ) / 4 = 2.6 cm² = 260 mm² donc pas de problème
Contrôle au flambage:
Allongement = 25 / 2.5 = 10
Coefficient de fixation = 1
Pas de correction au flambage pour un allongement < 12 pour le métal.
C.2) Epaisseur du tube minimum acceptée:
Le vis de diamètre 0.8 cm pourrait rentrer dans l'aluminium et ovaliser le trou ou déchirer le tube.
e = F / ( d x contrainte de refoulement) or la contrainte de refoulement = 2 x la contrainte de
cisaillement. La contrainte de cisaillement = 4/5 de la contrainte de traction vue ci dessus.
Contrainte de refoulement = 2 x (4/5 x 11 000) = 17 600 N
Epaisseur = 4074 / ( 0.8 x 17 600 ) = 0.29 cm = 2.9 mm Or nous avons 4 mm x 2 côtés = 8 mm
d'où pas de problème.
C.3) Flexion horizontale de la lyre:
Mf = ( 1178 x 25 x 25 ) / 50 = 14 725 Ncm
I / V = 14 725 / 11 000 = 1.34 cm³
Le I / V de ce tube doublé est de ; 3.14 x e x r² = 3.14 x 0.4 x 1.05² = 1.4 cm³ donc pas de problème.
Présentation Cager un parapente Evolution des modèles Détails techniques Calculs de résistance