PFG Technologie
 

Calcul et réalisation du transformateur à 20 kHz:

Documentation théorique click ici

Ci-dessus, le transformateur bobiné par nos soins.

Données utilisée du tore R58:

1) Choix du tore:

Tores en ferrite toroïdal R58 (voir doc. ci-dessous):

     détails techniques

Données utilisée du tore R58:

-Section:152 mm²

-Perméabilité relative du tore µr = 4300

-Perméabilité du vide µo = 4 x ∏ / 10000000

-Saturation du noyau en ferrite = 0.3 Tesla

2) Calcul des caractéristiques et essai du primaire:

A) Calcul du nombre de spires au primaire

N1 = V1 / (4.44 x f x Bmax. x S)

N1 = nombre de spires au primaire

V1 = tension primaire

f = fréquence en Hz

Bmax. = induction magnétique max (inférieure à la saturation)

S = section du tore

N1 = 12 / (4.44 x 20 000 x 0.25 x 0.000 152) = 4 spires

Etonnant par rapport aux 200 spires du brevet...

Les essais démontrerons la véracité ou non de ce calcul.

On peut voir les 4 spires bobinées à droite, au dessus un secondaire de 600 spires et en dessous un secondaire de 200 spires.

B) Calcul du courant nécessaire pour obtenir la saturation du tore (à ne jamais atteindre)

B = (µo x µr x N x I) / (2 x ∏ x r)  r est le rayon du tore en m

d'ou:

I = (B x 2 x ∏ x r) /  µo x µr x N

I = (0.25 x 2 x ∏ x 0.025) / ((4 x ∏ / 10000000) x 4300 x 4) = 1.86 A (à titre indicatif)

C) Calcul de la réactance du primaire à 20 000 Hz

Xl = 2 x ∏ x f x L

L = 0.000 043 Henrys (mesurée avec un appareil de mesure)

Xl = 2 x 3.14 x 20 000 x 0.000 043 = 5.4 Ω

d) Essais:

vue d'ensemble                                                  vue du transfo

Signal de commande du transistor à 20 000 Hz

Le courant mesuré est de 0.54 A sans résistance additionnelle.Le signal est plus propre pour un courant de 0.4 A. Le primaire oscille naturellement vers 25 000 Hz et l'ajout d'un condensateur de 0.6 uf en parallèle  permet de l'accorder à 20 000 Hz. le signal est en résonance et la tension est plus élevée.

 Signal au primaire non accordé               Signal du primaire accordé

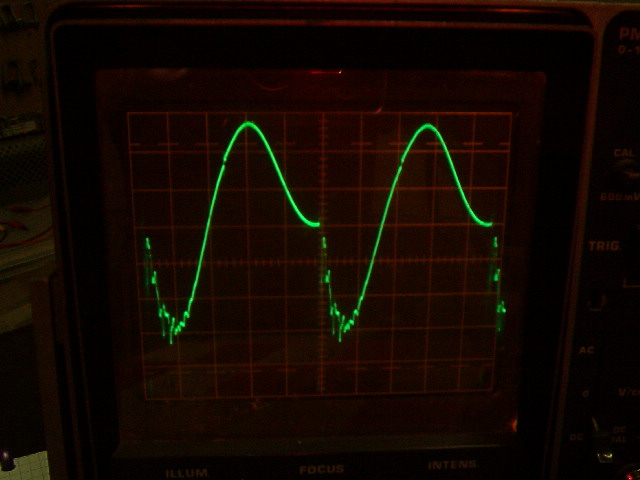
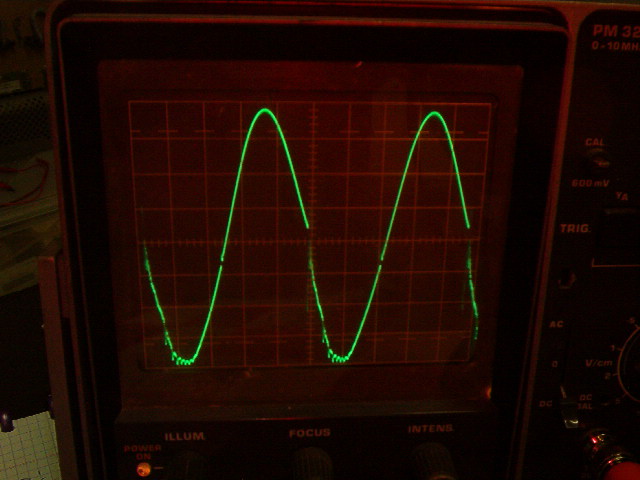
Tension crète-crète = 35 V  d'où  Tension efficace = 12.5 V

U eff = Ucc / (2 x √2)

La puissance au primaire est de 12,5 v x 0.4 A = 5W

2) Calcul des caractéristiques et essai du secondaire:

Avec 200 spires, nous devrions avoir 200/4 = 50 fois plus de tension soit 50 x 12.5 = 625 Vef ou 35 x 50 = 1750 Vcc

Imax = 0.4 / 50 = 0.008 A (sans tenir compte du rendement)

Il est impératif de rester sous cette valeur pour faire l'essais en charge du secondaire car si on demande plus que la puissance d'entrée - les pertes le signal au secondaire s'écroulera.

Calcul de la résistance à mettre au secondaire: R = U / I   = 625 / 0.008 = 78 125 Ω

Essais avec R = 81 000 Ω:

Secondaire en charge primaire accordé                Secondaire en charge primaire non accordé

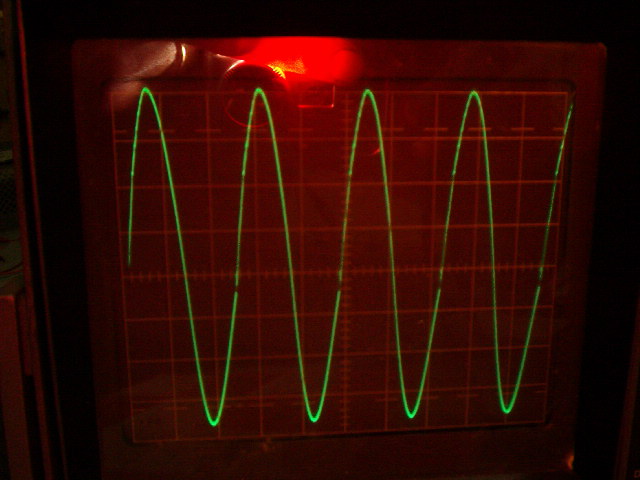
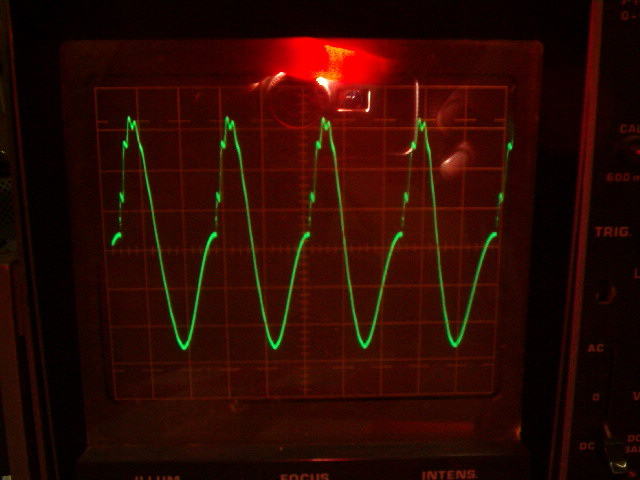
Ucc est à 800 V en limitant le courant à 0.2 A du coté primaire avec une résistance additionnelle car le bobinage de 600 spires crache des arcs électriques si on monte plus haut.

Le transfo fonctionne très bien car avec un courant primaire de 0.4 A réduit à 0.2 A, la tension est également réduite au primaire d'environ la moitié. Nous avons 800 V au lieu de 1750 V calculée soit environ la moitié en pleine charge.

Signal secondaire en charge avec temps mort         idem après redresseur 4 diodes

4) Réflexion et conclusion provisoire:

Cela prouve que la fabrication et le calcul du transfo. semble correct.

Le fait d'accorder le primaire semble également nécessaire.

Les 200 spires coté secondaire correspondent à un chiffre de Meyer, mais pour ce qui est du primaire ???

Ce transfo. peut fonctionner sur une résistance de 81 kΩ mai sur un cellule à eau de quelques dizaine d'Ω le signal chutera .

Se sera pour la suite mais les examens arrivent et j'ai du travail, se sera pour un peu plus tard.il faudra voir avec le circuit résonnant. Bref à suivre...

PFG Technologie