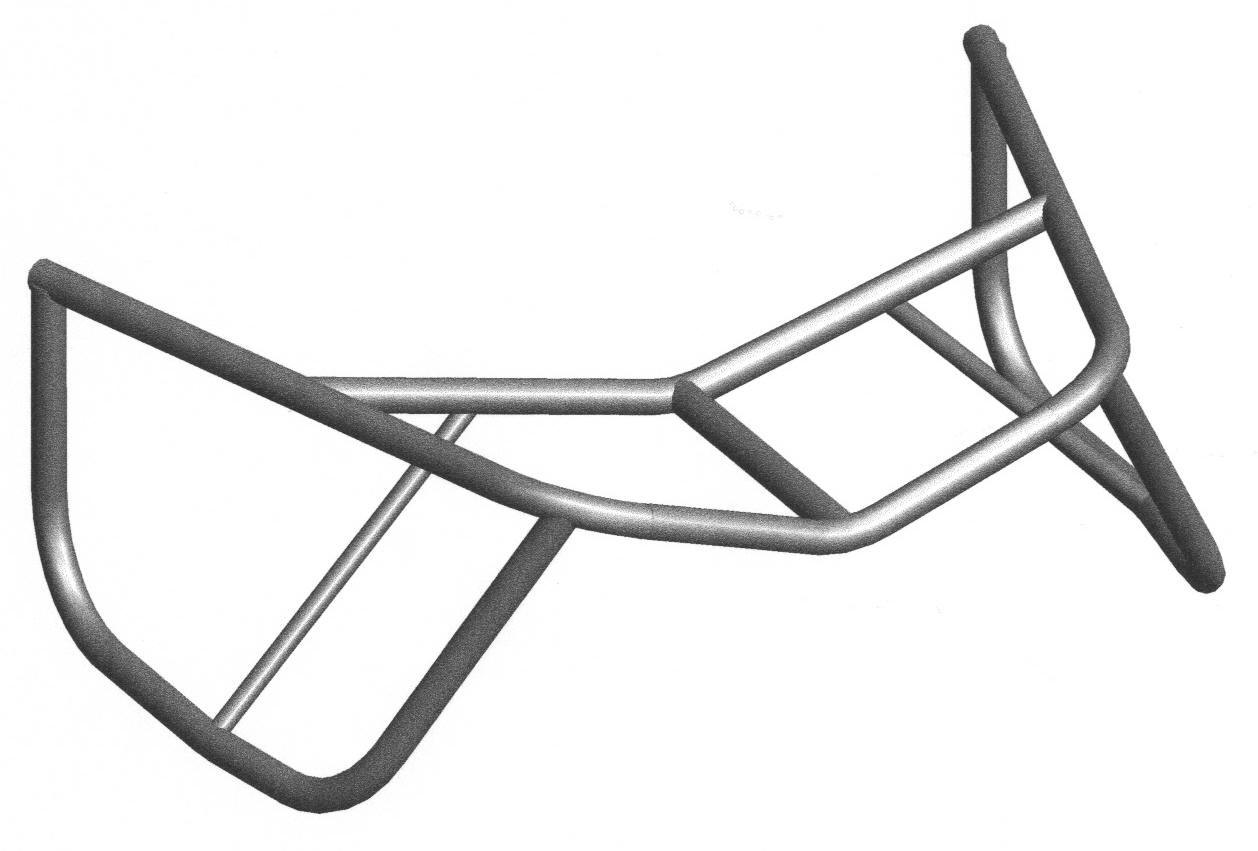
Calculs du cadre:
Calcul du cadre dans le sens droite gauche:
Prenons une charge de fonctionnement maximum de 6 g sans détérioration du cadre, soit 600 kg.(8g en rupture)
Pour une Boréa, le centrage est de 8 cm sur 50 cm soit:
42/50 = 84 % de la charge sur l'avant. 600 x 0.84 = 504 kg.
8 /50 = 16 % de la charge sur l'arrière. 600 x 0.16 = 96 kg.
Calculons donc l'avant en flexion:
Données: charge au centre : 504 kg. ou 5040 Newtons
portée : 40 cm. d'axe en axe.
Pour de l'aluminium:
Résistance élastique de l'aluminium AlMgSi 0.5 F22 / 6060 = 16 000 N/cm² (21 500 N/cm² en rupture)
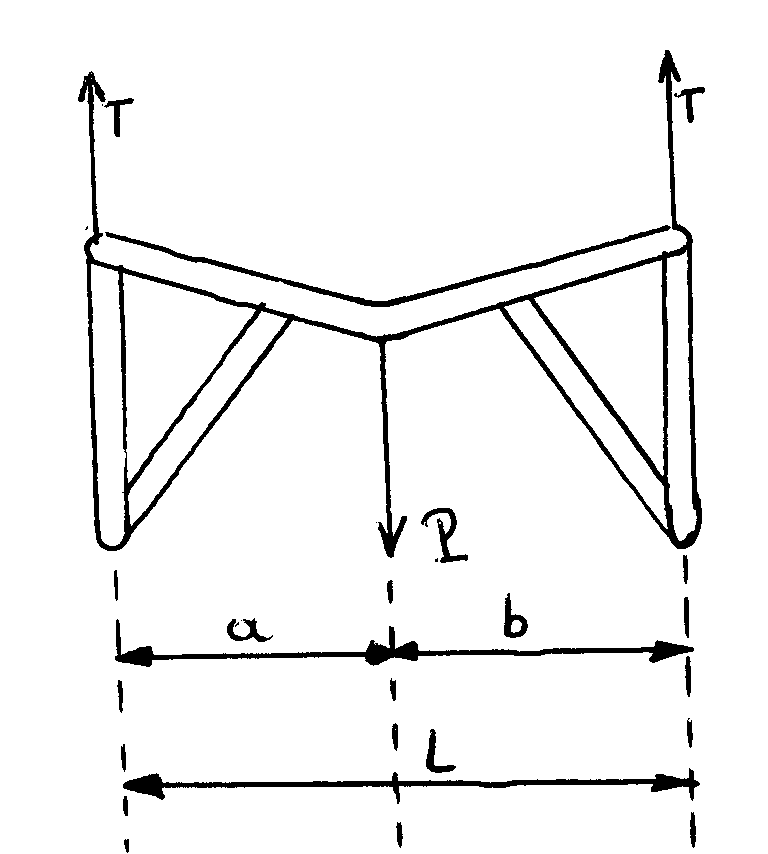
Rappel: a = distance du point d'appui gauche à la force locale en cm.
b = distance du point d'appui droit à la force locale en cm.
L = longueur entre appuis en cm.
P = Force locale en Newtons.
Moment fléchissant : Mf = P x a x b / L = 5040 x 20 x 20 / 40 = 50 400 Ncm
I/V = Mf / contrainte = 50 400 / 16 000 = 3.15 cm³
Pour de l'acier inox:
Résistance élastique de l'inox 50 000 N/cm² (70 000 N/cm² en rupture)
Moment fléchissant : Mf = P x a x b / L = 5040 x 20 x 20 / 40 = 50 400 Ncm
I/V = Mf / contrainte = 50 400 / 50 000 = 1.008 cm³
L'acier inox est donc 3.15 / 1.008 = 3.12 fois plus résistant que ce type d'alliage d'aluminium.
L'intérêt de cet aluminium est sa bonne soudabilité et son cintrage aisé.
Le dural, est un alliage d'aluminium difficilement soudable et cintrable mais possède une résistance proche de l'acier.
Déterminons le tube nécessaire:
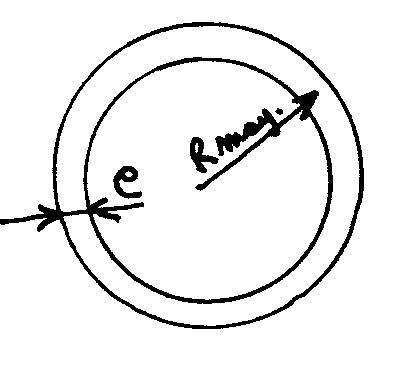
Le I / V d'un tube circulaire est égal à ( 3.14 x R² x e ) avec e = l'épaisseur du tube et R le rayon moyen en cm.
Un tube en aluminium de 25 x 2 mm à un I / V = 3.14 x 1.15² x 0.2 = 0.83 cm³ trop faible seul.
Un tube d'acier inox de 20 x 2mm à un I / V = 3.14 x 0.9² x 0.2 = 0.5 cm³ trop faible seul.
Première solution:(utilisée dans le cadre 2005)
Insérer un tube inox de 20 x 2mm dans le tube en aluminium 25 x 2mm uniquement où c'est nécessaire.
Deuxième solution : triangulation :
Avantage : gain de poids.
Inconvénient : moins esthétique
Troisième solution : Le titane.
Trop cher.
Calcul du cadre dans le sens avant arrière:
Dans ce sens, le cadre force moins pour les raisons suivantes:
- La charge de chaque côté est de 300 kg et répartie sur la longueur.
- le tube est soutenu plus ou moins en son centre.(Portée diminuée de moitié soit: 22.5 cm)
- les lyres participent à la rigidité de l'ensemble.
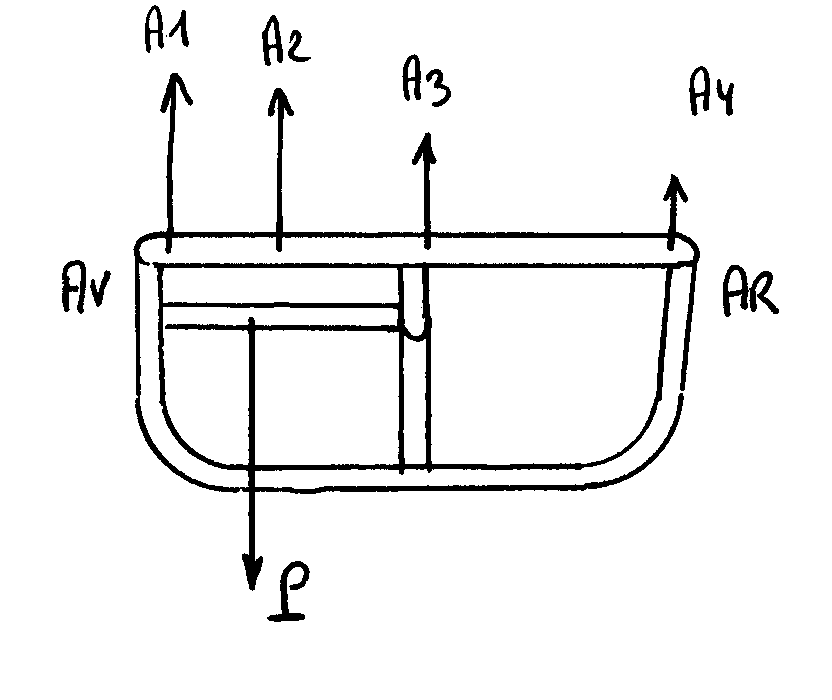
Pour de l'aluminium:
Résistance élastique de l'aluminium AlMgSi 0.5 F22 / 6060 = 16 000 N/cm² (21 500 N/cm² en rupture)
Rappel: dans ce cas, P est la charge répartie en Newtons par cm de tube et plus la charge locale.
P = F / L = 3000 / 45 = 66.6 N/cm (charge répartie)
La formule du moment fléchissant n'est plus la même que pour une charge locale.
Moment fléchissant : Mf = P x L² / 8 = 66.6 x (45/2)² / 8 = 4215 Ncm
I/V = Mf / contrainte = 4215 / 16 000 = 0.26 cm³
Un tube en aluminium de 25 x 2 mm à un I / V = 3.14 x 1.15² x 0.2 = 0.83 cm³
Donc le tube seul est déjà trois fois trop solide.
Un tube 20 x 2 fait 0.5 cm³ de I / V et serait déjà bien suffisant.
Calcul du tube de suspension du pilote:
longueur : 25 cm
charge à 5.5 cm de l'extrémité
Pour de l'aluminium:
Résistance élastique de l'aluminium AlMgSi 0.5 F22 / 6060 = 16 000 N/cm² (21 500 N/cm² en rupture)
Moment fléchissant : Mf = P x a x b / L = 6000 x 5.5 x 19.5 / 25 = 25 740 Ncm
I/V = Mf / contrainte = 25 740 / 16 000 = 1.6 cm³
Pour de l'acier inox:
Résistance élastique de l'inox 50 000 N/cm² (70 000 N/cm² en rupture)
Moment fléchissant : Mf = P x a x b / L = 6000 x 5.5 x 19.5 / 25 = 25 740 Ncm
I/V = Mf / contrainte = 25 740 / 50 000 = 0.5 cm³
Déterminons le tube nécessaire:
Le I / V d'un tube circulaire est égal à ( 3.14 x R² x e ) avec e = l'épaisseur du tube et R le rayon moyen en cm.
Un tube en aluminium de 25 x 2 mm à un I / V = 3.14 x 1.15² x 0.2 = 0.83 cm³ trop faible
Un tube d'acier inox de 20 x 2mm à un I / V = 3.14 x 0.9² x 0.2 = 0.5 cm³ serait suffisant seul.
Un tube d'acier inox de 20 x 1.5mm à un I / V = 3.14 x 0.9² x 0.15 = 0.38 cm³
Première solution:(utilisée dans le cadre 2005)
Insérer un tube inox de 20 x 1.5 dans le tube en aluminium 25 x 2
Calcul d'une soudure sur un tube alu. 25 x 2mm:
Remarque: coefficient de résistance pour les soudures en bout = 0.75
Longueur de la soudure : 25 mm x 3.14 = 78.5 mm
Epaisseur minimum = 2 mm
Contrainte de cisaillement : 4/5 de la contrainte de traction.
Contrainte élastique de traction ou de compression de la soudure : 110 N/mm²
Contrainte élastique de cisaillement : 4/5 x 110 = 88 N/ mm²
Résistance de la soudure en cisaillement : (cas du tube de suspension du pilote)
S = 2 x 78.5 mm = 157 mm²
Résistance au cisaillement : 88 x 157 = 13 816 N x coéf (0.75) = 10 362 N soit 1036 kg. pour une seule soudure.
Résistance de la soudure en traction ou compression: (cas des lyres)
S = 2 x 78.5 mm = 157 mm²
Résistance au cisaillement : 110 x 157 = 17 270 N x coéf (0.75) = 12 953 N soit 1295 kg pour une seule soudure.
La soudure la plus sollicitée est la soudure avant du tube de suspension du pilote.
La charge sur cette soudure à 6 g serait de 6000 x 19.5/25 = 4680 N soit 468 Kg.
La soudure peut tenir sans dommage à 10 362 Newtons soit 1036 kg.
Donc pas de problème.